解方程怎么解？

解方程怎么解？

使方程左右两边相等的未知数的值，叫做方程的解。求方程的解的过程叫做解方程。

必须含有未知数等式的等式才叫方程。

等式不一定是方程，方程一定是等式。方法⒈估算法：刚学解方程时的入门方法。直接估计方程的解，然后代入原方程验证。⒉应用等式的性质进行解方程。

⒊合并同类项：使方程变形为单项式⒋移项：将含未知数的项移到左边，常数项移到右边例如：⒌去括号：运用去括号法则，将方程中的括号去掉。 6.公式法：有一些方程，已经研究出解的一般形式，成为固定的公式，可以直接利用公式。可解的多元高次的方程一般都有公式可循。

7.函数图像法：利用方程的解为两个以上关联函数图像的交点的几何意义求解。方程是正向思维。步骤⑴有分母先去分母⑵有括号就去括号⑶需要移项就进行移项⑷合并同类项⑸系数化为1求得未知数的值⑹ 开头要写“解”例如:解这道题首先要知道等于几， 不过，x不一定放在方程左边，或一个方程式子里有两个x，这样就要用数学中的简便计算方法去解决它了。

有些式子右边有x，为了简便算，可以调换位置。

怎么解方程

解分数方程的方法如下：1、看等号两边是否可以直接计算。2、如果两边不可以直接计算，就运用和差积商的公式对方程进行变形。

3、对可以相加减的项进行通分。

4、两边同时除以一个不为零的数。注意：（1）、都含有未知数的项才能相加减，或者都不含有未知数的项才能相加减。（2）、除以一个数等于乘以这个数的倒数。解方程依据：1、移项变号：把方程中的某些项带着前面的符号从方程的一边移到另一边，并且加变减，减变加，乘变除以，除以变乘。

2、等式的基本性质。性质1：等式两边同时加(或减)同一个数或同一个代数式，所得的结果仍是等式。用字母表示为：若a=b，c为一个数或一个代数式。

a+c=b+c。a-c=b-c。性质2：等式的两边同时乘或除以同一个不为0的数,所得的结果仍是等式。

用字母表示为：若a=b，c为一个数或一个代数式（不为0）。则：a×c=b×c 或a/c=b/c性质3：若a=b，则b=a（等式的对称性）。性质4：若a=b，b=c则a=c（等式的传递性）。

解方程有几种方法？如何才能轻松求解？

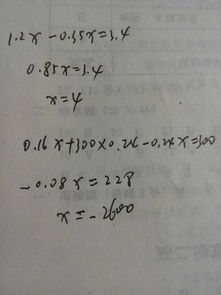
在上小学的时候，很多学生都会接触到加法、乘法、除法和减法，在上小学高年级的时候，比如说五六年级就有可能接触到方程。对于小学生来说方程是比较难的，但是如果你掌握到解方程的技巧，也能够轻松的把方程解出来。

那你知道解方程有几种方法吗？如何才能够轻松求解呢？公式法求解公式法解方程是最简单的，可以先用配方法把方程配成一元二次的方程，然后就能够求解了。

在用公式法解方程之后，就能够很快的得到方程的答案，并且这种方法也是最简单易掌握的，特别适合初学者。在配方的时候，如果你加了多少树，最后就要剪出多少数，所以你要观察这个方程，然后找出最合适的配方法，去进行配方。因式分解法因式分解法是比较难的，很多学生都不会这种方法，但是如果你掌握这种方法就能够解大部分的方程。第1步将方程的右边化为0，第2步将方程的左边分解为两个因式的乘积。

第3步令每个一次式分别为0，得到两个一元一次方程，第4步，两个一元一次方程的解，就是所求一元二次方程的解。因式分解法是比较灵活的，并且能够把大部分方程的解求出来，如果你能够学会因式分解法，就能够让思维更加活跃，也能够提高自己的运算能力。所以你也可以观看一些教学视频，把因式分解法的规律掌握住，这样就能够灵活的运用因式分解法解方程。

总结所以虽然方程比较难，但是如果你掌握了正确的方法，就能够用不同的方法将这个方程解出来。在学习数学的时候，不要想着一口吃成胖子，应该一步一步的学习，将基础打好之后才能够把比较难的题解出来。

解方程怎么解

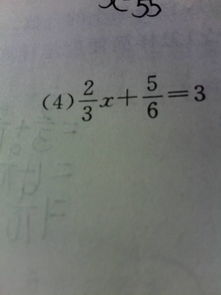
1、有分母先去分母。2、有括号就去括号。

3、需要移项就进行移项。

4、合并同类项。5、系数化为1求得未知数的值。6、开头要写“解”。 方程的相关概念 1.含有未知数的等式叫方程，也可以说是含有未知数的等式是方程。

2.使等式成立的未知数的值，称为方程的解，或方程的根。 3.解方程就是求出方程中所有未知数的值的过程。 4.方程一定是等式，等式不一定是方程。

不含未知数的等式不是方程。 5.验证：一般解方程之后，需要进行验证。验证就是将解得的未知数的值代入原方程，看看方程两边是否相等。

如果相等，那么所求得的值就是方程的解。 6.注意事项：写“解”字，等号对齐，检验。