共轭复根怎么求

共轭复根的求法：对于ax²+bx+c=0（a≠0）若Δ<0，该方程在实数域内无解，但在虚数域内有两个共轭复根，为共轭复根是一对特殊根。指多项式或代数方程的一类成对出现的根。

若非实复数α是实系数n次方程f(x)=0的根，则其共轭复数α*也是方程f(x)=0的根，且α与α*的重数相同，则称α与α*是该方程的一对共轭复（虚）根。

举例：r*r+2r+5=0，求它的共轭复根。解答过程：（1）r*r+2r+5=0，其中a=1，b=2，c=5。（2）判别式△=b²-4ac=4-20=-16=(±4i)²。（3）所以r=(-2±4i)/2=-1±2i。

扩展资料：一元二次方程的一般形式如下：确定判别式，计算Δ=b²-4ac（希腊字母，音译为戴尔塔）。

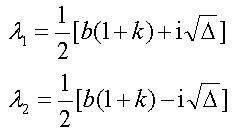
具体如图：根据一元二次方程求根公式韦达定理：，当时，方程无实根，但在复数范围内有2个复根。复根的求法为（其中是复数，）。

由于共轭复数的定义是形如的形式，称与为共轭复数。

另一种表达方法可用向量法表达：，。其中，tanΩ=b/a。由于一元二次方程的两根满足上述形式，故一元二次方程在时的两根为共轭复根。根与系数关系：，。

扩展资料：共轭复根经常出现于一元二次方程中，若用公式法解得根的判别式小于零，则该方程的根为一对共轭复根。复数的加法法则：设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

两个复数的和依然是复数。

复数共轭是指a+bi与a-bi,这里a,b都是实数. 产生这对共轭复根的二次方程为k[(x-a)^2+b^2]=0 一般的实系数二次方程,ax^2+bx+c=0,当判别式△=b^2-4ac

继续浏览：