如何证明面面垂直？

定义：若两个平面的二面角为直二面角(平面角是直角的二面角)，则这两个平面互相垂直。定理一个平面过另一平面的垂线，则这两个平面相互垂直。

几何描述:若a⊥β，a⊂α，则α⊥β证明:任意两个平面关系为相交或平行，设a⊥β，垂足为P，那么P∈β∵a⊂α，P∈a∴P∈α即α和β有公共点P，因此α与β相交。

设α∩β=b，∵P是α和β的公共点∴P∈b过P在β内作c⊥b∵b⊂β，a⊥β∴a⊥b，垂足为P又c⊥b，垂足为P∴∠aPc是二面角α-b-β的平面角∵c⊂β∴a⊥c，即∠aPc=90°根据面面垂直的定义，α⊥β推论1如果一个平面的垂线平行于另一个平面，那么这两个平面互相垂直。已知α⊥a，a∥β，求证α⊥β证明:过a任意作一个平面γ与β相交，设交线为c∵a∥β∴a∥c(线面平行的性质定理)∵a⊥α∴c⊥α(线面垂直的性质定理)∵c⊂β∴β⊥α(定理1)推论2如果两个平面的垂线互相垂直，那么这两个平面互相垂直。(可理解为法向量垂直的平面互相垂直)证明:设有a⊥α，b⊥β，且a⊥b则根据线面平行的判定定理，有a∥β∵a⊥α∴α⊥β(推论1)这些定理和推论都是向量法解题的基础，例如向量法解得一个平面的法向量与另一个平面平行，那么这两个平面就垂直。三个两两垂直的平面的交线两两垂直。

面面垂直的证明方法有哪些

证明面面垂直的基本方法有：（1）利用定义证明，即利用两平面相交成直二面角来证明；（2）利用面面垂直的判定定理证明，即若a⊥ ，a ，则 ⊥ 在证明两平面垂直时，一般方法是先从现有的直线中寻找平面的垂线，若没有这样的直线，则可通过作辅助线来解决，而作辅助线则应有理论根据并且要有利于证明，不能随意添加.在有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直.解决这类问题的关键是熟练掌握

证面面垂直有哪些方法

1。证明平面与平面垂直的方法：（1）利用定义：证明二面角的平面角为直角；（2）利用“面面垂直”判定定理：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。简述为：“若线面垂直，则面面垂直”。2.平面与平面垂直的性质：（1）两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。简述为：“若面面垂直，则线面垂直”。（2）如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内。此性质可以作为面面垂直的性质定理直接应用3．“面面垂直”的判定定理和性质定理和“线面垂直”的判定定理和性质定理有密切联系，若注意到这一联系，则既可加深对垂直关系概念的系统理解，又可加强对有垂直关系的有关定理之间的内在联系的认识。例题：如图，过s引三条长度相等但不共面的线段sa、sb、sc，且∠asb=∠asc=60°，∠bsc=90°。求证：平面abc⊥平面bsc。作ad⊥平面bsc，d为垂足。∵∠asb=∠asc=60°，sa=sb=sc，则as=ab=ac，∴d为△bsc的外心。又∠bsc=90°，∴d为bc的中点，即ad在平面abc内。∴平面abc⊥平面bsc。证法二：取bc的中点d，连接ad、sd，易证ad⊥bc，又△abs是正三角形，△bsc为等腰直角三角形，∴bd=sd∴ad2+sd2=ad2+bd2=ab2=as2，由勾股定理的逆定理，知ad⊥sd，∴ad⊥平面bsc。又ad平面abc，∴平面abc⊥平面bsc。评注本题是证明面面垂直的典型例题，关键是将证明“面面垂直”问题转化为证明“线面垂直”。方法一是作平面的垂线而后证明它在另一个平面内；方法二则是在一个平面内找一条线段，证明它与另一个平面垂直。我在网上找的，你看看行不？证明平面与平面垂直的方法：（1）利用定义：证明二面角的平面角为直角；（2）利用“面面垂直”判定定理：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。

简述为：“若线面垂直，则面面垂直”。

2.平面与平面垂直的性质：（1）两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。简述为：“若面面垂直，则线面垂直”。（2）如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内。此性质可以作为面面垂直的性质定理直接应用3．“面面垂直”的判定定理和性质定理和“线面垂直”的判定定理和性质定理有密切联系，若注意到这一联系，则既可加深对垂直关系概念的系统理解，又可加强对有垂直关系的有关定理之间的内在联系的认识。

例题：如图，过s引三条长度相等但不共面的线段sa、sb、sc，且∠asb=∠asc=60°，∠bsc=90°。求证：平面abc⊥平面bsc。作ad⊥平面bsc，d为垂足。

∵∠asb=∠asc=60°，sa=sb=sc，则as=ab=ac，∴d为△bsc的外心。又∠bsc=90°，∴d为bc的中点，即ad在平面abc内。∴平面abc⊥平面bsc。

证法二：取bc的中点d，连接ad、sd，易证ad⊥bc，又△abs是正三角形，△bsc为等腰直角三角形，∴bd=sd∴ad2+sd2=ad2+bd2=ab2=as2，由勾股定理的逆定理，知ad⊥sd，∴ad⊥平面bsc。又ad平面abc，∴平面abc⊥平面bsc。评注本题是证明面面垂直的典型例题，关键是将证明“面面垂直”问题转化为证明“线面垂直”。

方法一是作平面的垂线而后证明它在另一个平面内；方法二则是在一个平面内找一条线段，证明它与另一个平面垂直。

面面垂直的证明方法

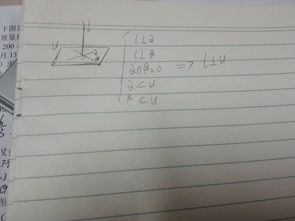
一个平面过另一平面的垂线，则这两个平面相互垂直。如果一个平面的垂线平行于另一个平面，那么这两个平面互相垂直。

如果两个平面的垂线互相垂直，那么这两个平面互相垂直（可理解为法向量垂直的平面互相垂直）。

1.如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。 2.如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。 3.如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面。推论：三个两两垂直的平面的交线两两垂直。

4.如果两个平面互相垂直，那么一个平面的垂线与另一个平面平行。（判定定理推论1的逆定理）推论：如果两个平面互相垂直，那么分别垂直于这两个平面的两条垂线也互相垂直。

证明两个面垂直的方法(如何证明面面垂直?)

1、证明面面垂直四个方法。 2、证明面面垂直有几种方法。

3、面面垂直的证明方法总结。

4、怎么证明两面垂直。1.证明面面垂直四个方法是利用定义证明、利用面面垂直的判定定理证明、判定定理法、向量定理，若两个平面的二面角为直二面角（平面角是直角的二面角），则这两个平面互相垂直。 2.平面角由射线、点、射线构成，是从平面内一点出发的两条射线（半直线）所组成的图形。 3.平面角的大小定义为以两射线交点为圆心的圆被射线所截的弧长和半径之比。

继续浏览：