解三次方程，怎么解？

三次方程怎么解

一元三次方程解法如下：强行开平方、开立方后计算出来，这个式子的值大约为5。用计算器分别计算两个三次根式的值，算到小数点后29位，可以发现小数部分是一模一样的（就算不一样，也仅仅是最后一位或两位）。

所以我们可以直接肯定，这两个根式的和就是5。

配方是根据三次项系数和二次项系数来配的。例如x³+6x²+x=10这个方程，三次项和二次项的系数分别为1和6，对应的完全立方式的一次项系数和常数项分别为12和8，所以在方程两边加上11x+8，得到：x³+6x²+12x+8=11x+18即(x+2)³=11x+18右边的11x+18可以表示成11x+22-4=11(x+2)-4(x+2)³=11(x+2)-4这和二次方程很不一样。二次方程配方后只有左边有x，可以两边开平方求解。三次方程配方后，方程的两边都有x，所以无法直接开立方求解，我们必须要寻找新方法解出x+2的值才行（这个所谓的新方法就是卡丹公式法）。

三次方程怎么解?

解方程的方法：1、估算法：刚学解方程时的入门方法。直接估计方程的解，然后代入原方程验证。

2、应用等式的性质进行解方程。

3、合并同类项：使方程变形为单项式4、移项：将含未知数的项移到左边，常数项移到右边例如：3+x=18解：x=18-3x=15解方程依据1、移项变号：把方程中的某些项带着前面的符号从方程的一边移到另一边，并且加变减，减变加，乘变除以，除以变乘；2、等式的基本性质性质1：等式两边同时加(或减)同一个数或同一个代数式，所得的结果仍是等式。用字母表示为：若a=b，c为一个数或一个代数式。(1)a+c=b+c(2)a-c=b-c性质2：等式的两边同时乘或除以同一个不为0的数，所得的结果仍是等式。用字母表示为：若a=b，c为一个数或一个代数式（不为0）。

则：a×c=b×c 或a/c=b/c性质3：若a=b，则b=a（等式的对称性）。性质4：若a=b，b=c则a=c（等式的传递性）。

如何求解3次方程？

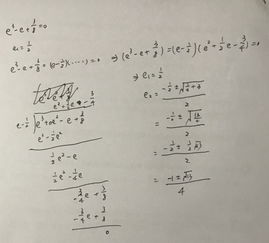解:设一般的一元三次方程为 x^3+ax^2+bx+c=0令 x=y-a/3,代入得(y-a/3)^3+a(y-a/3)^2+b(y-a/3)+c=0展开化简得 y^3+(b-a^2/3)y+(2a^3/27-ab/3+c)=0这就变成了缺二次项的三次方程.因此解一般的三次方程可归结为解形如 x^3+px+q=0 的方程.令x=u+v,上式变为u^3+v^3+q+(3uv+p)(u+v)=0为了求出u,v,只须设 3uv+p=0,从而有u^3+v^3+q=0.这就只要解方程组:u^3+v^3=-q..................(1)(u^3)(v^3)=-p^3/27..........(2)由韦达定理可知 u^3,v^3是二次方程 t^2+qt-p^3/27=0的根,解此方程得u^3=t1=[-q+√(q^2+4p^3/27)]/2=-(q/2)+√[(q^2)/4+p^3/27]v^3=t2=-(q/2)-√[(q^2)/4+p^3/27]由于u和v的立方根各有三种取法(把u^3和v^3写成复数的三角形式, 然后开立方),因而可得u+v的九组值,但九组值中只有三组满足条件: 3uv+p=0.这三组才是原方程的根.这样我们便得到用三次方程的系数表示根的公式:x=u+v= [-q/2+√(q^2/4+p^3/27)]^(1/3)+[-q/2-√(q^2/4+p^3/27)]^(1/3)即是所谓的卡当公式.(此公式不好用,一般都不用它).例:解方程 x^3+3x^2-3x-14=0解:令x=y-1, 方程化为 y^3-6y-9=0(由此可知y=3是它的一个实数根,因而可分解因式为(y-3)(y^2+3y+3)=0.若知道这麽解,下面的过程就可全省去.作为上述解法的实例,我不用此法,继续往下作.)又设y=u+v,则得u^3+v^3-9+(3uv-6)(u+v)=0令3uv-6=0,故u^3+v^3-9=0∴得方程组: (u^3)(v^3)=8........(1)u^3+v^3=9...........(2)由韦达定理可得二次方程t^2-9t+8=(t-8)(t-1)=0,即u^3=8,v^3=1.写成复数形式:u^3=8(cos0°+isin0°)v^3=cos0°+isin0°于是u=2[cos(k*360°/3)+isin(k*360°/3)]v=cos(k*360°/3)+isin(k*360°/3)(k=o,1,2)故u1=2, u2=2ω, u3=2ω^2, 其中ω=-1/2+i√3/2v1=1, v2=ω^2, v3=ω.(∵u1*v1=2; u2*v2=2ω^3=2*1=2; u3*v3=2ω^3=2,满足3uv-6=0)∴y1=u1+v1=2+1=3; y2=u2+v2=2ω+ω^2=-3/2+i√3/2;y3=u3+v3=2ω^2+ω=-3/2-i√3/2.因此原方程的根为:x1=y1-1=3-1=2; x2=y2-1=-5/2+i√3/2; x3=y3-1=-5/2-i√3/2.从上面可以看出三次方程确实可解,但这种解法并不一定是简捷的.特别是,如果方程有有理根,那么先用综合除法找出有理根会更方便些

怎么解三次方程

法1：能做因式分解的，将算式因式分解得到=0的式子，假设依次得0，可得结果法2:：，无法因式分解的一元三次方程的求根公式用通常的演绎思维是作不出来的，用类似解一元二次方程的求根公式的配方法只能将型如aX^3＋bX^2＋cX＋d=0的标准型一元三次方程形式化为X^3＋pX＋q=0的特殊型。卡尔丹公式 一元三次方程X^3＋pX＋q=0 (p、q∈R) 判别式Δ=(q/2)^2＋(p/3)^3 【卡尔丹公式】 X1=(Y1)^(1/3)＋(Y2)^(1/3)； X2= (Y1)^(1/3)ω＋(Y2)^(1/3)ω^2； X3=(Y1)(1/3)ω^2＋(Y2)^(1/3)ω， 其中ω=(－1＋i3^(1/2))/2； Y(1,2)=－(q/2)±((q/2)^2＋(p/3)^3)^(1/2)。

一般式一元三次方程aX ^3＋bX ^2＋cX＋d=0 令X=Y—b/(3a)代入上式， 可化为适合卡尔丹公式求解的特殊型三次方程Y^3＋pY＋q=0。

盛金公式 三次方程应用广泛。用根号解一元三次方程，虽然有著名的卡尔丹公式，并有相应的判别法，但使用卡尔丹公式解题比较复杂，缺乏直观性。范盛金推导出一套直接用a、b、c、d表达的较简明形式的一元三次方程的一般式新求根公式，并建立了新判别法。 【盛金公式】 一元三次方程aX^3＋bX^2＋cX＋d=0，（a，b，c，d∈R，且a≠0）。

重根判别式： A=b^2－3ac； B=bc－9ad； C=c^2－3bd， 总判别式： Δ=B^2－4AC。 当A=B=0时，盛金公式①： X⑴=X⑵=X⑶=－b/(3a)=－c/b=－3d/c。 当Δ=B^2－4AC>0时，盛金公式②： X⑴=(－b－Y⑴^(1/3)－Y⑵^(1/3))/(3a)； X(2，3)=(－2b＋Y⑴^(1/3)＋Y⑵^(1/3))/(6a)±i3^(1/2)(Y⑴^(1/3)－Y⑵^(1/3))/(6a)； 其中Y(1，2)=Ab＋3a(－B±(B^2－4AC)^(1/2))/2，i^2=－1。

当Δ=B^2－4AC=0时，盛金公式③： X⑴=－b/a＋K；X⑵=X3=－K/2， 其中K=B/A，(A≠0)。 当Δ=B^2－4AC(2A^(3/2))，(A>0，－1<T0时，方程有一个实根和一对共轭虚根； ③：当Δ=B^2－4AC=0时，方程有三个实根，其中有一个两重根； ④：当Δ=B^2－4AC<0时，方程有三个不相等的实根。 【盛金定理】 当b=0，c=0时，盛金公式①无意义；当A=0时，盛金公式③无意义；当A≤0时，盛金公式④无意义；当T＜-1或T＞1时，盛金公式④无意义。

当b=0，c=0时，盛金公式①是否成立？盛金公式③与盛金公式④是否存在A≤0的值？盛金公式④是否存在T＜-1或T＞1的值？盛金定理给出如下回答： 盛金定理1：当A=B=0时，若b=0，则必定有c=d=0（此时，方程有一个三重实根0，盛金公式①仍成立）。 盛金定理2：当A=B=0时，若b≠0，则必定有c≠0（此时,适用盛金公式①解题）。 盛金定理3：当A=B=0时，则必定有C=0（此时,适用盛金公式①解题）。

盛金定理4：当A=0时，若B≠0，则必定有Δ＞0（此时，适用盛金公式②解题）。 盛金定理5：当A＜0时，则必定有Δ＞0（此时，适用盛金公式②解题）。 盛金定理6：当Δ=0时，若B=0，则必定有A=0（此时，适用盛金公式①解题）。 盛金定理7：当Δ=0时，若B≠0，盛金公式③一定不存在A≤0的值（此时，适用盛金公式③解题）。

盛金定理8：当Δ＜0时，盛金公式④一定不存在A≤0的值。（此时，适用盛金公式④解题）。 盛金定理9：当Δ＜0时，盛金公式④一定不存在T≤-1或T≥1的值，即T出现的值必定是-1＜T＜1。 显然，当A≤0时，都有相应的盛金公式解题。

注意：盛金定理逆之不一定成立。如：当Δ＞0时，不一定有A＜0。 盛金定理表明：盛金公式始终保持有意义。任意实系数的一元三次方程都可以运用盛金公式直观求解。

当Δ=0(d≠0)时，使用卡尔丹公式解题仍存在开立方（WhenΔ=0,Shengjin’s formula is not with radical sign, and efficiency higher for solving an equation）。与卡尔丹公式相比较，盛金公式的表达形式较简明，使用盛金公式解题较直观、效率较高；盛金判别法判别方程的解较直观。重根判别式A=b^2－3ac；B=bc－9ad；C=c^2－3bd是最简明的式子，由A、B、C构成的总判别式Δ=B^2－4AC也是最简明的式子（是非常美妙的式子），其形状与一元二次方程的根的判别式相同；盛金公式②中的式子(－B±(B^2－4AC)^(1/2))/2具有一元二次方程求根公式的形式，这些表达形式体现了数学的有序、对称、和谐与简洁美。

如何解三次方程

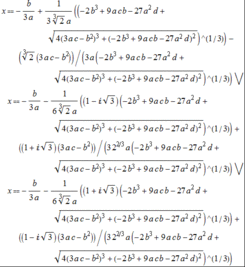一些特殊的三次方程可以通过分解因式求解，有一些需要去试根，拿±1，±2带进去试如果有幸被试到，那么原方程也可以分解因式法降为一个二次方程，就可以解决了！普通的三次方程的精确解法比较麻烦，大致思路是通过换元法化为特殊形式，求解