方向余弦计算公式

方向余弦计算公式

方向余弦计算公式：方向余弦=(x，y，z)/√(x²+y²+z²)，方向余弦是指在解析几何里，一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。

“方向余弦矩阵”是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。

方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。方向角的余弦称为有向线段或相应的有向线段的方向余弦。

方向余弦怎么求

设：A（x1,y1,z1）,B（x2,y2,z2），向量AB的方向余弦＝｛（x2-x1）/d,（y2-y1）/d.（z2-z1）/d｝，其中，d＝|AB|＝√[（x2-x1）²+（y2-y1）²+（z2-z1）²]，（x2-x1）/d＝cosα.（y2-y1）/d＝cosβ.（z2-z1）/d＝cosγ，其中：α,β,γ是向量AB分别与x轴。y轴，z轴所成的夹角[0≤α,β,γ≤π]。

方向余弦是指在解析几何里，一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。

两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。 “方向余弦矩阵”是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。 设有空间两点，若以P1为始点，另一点P2为终点的线段称为有向线段。

通过原点作一与其平行且同向的有向线段，将与Ox,Oy,Oz三个坐标轴正向夹角分别记作α,β,γ。这三个角α,β,γ称为有向线段的方向角，其中0≤α≤π,0≤β≤π,0≤γ≤π。若有向线段的方向确定了，则其方向角也是唯一确定的。

方向角的余弦称为有向线段或相应的有向线段的方向余弦。

向量的方向余弦怎么求

若有向量MN={x,y,z}，则向量MN的单位向量就为向量MN除以向量MN的模，α、β、γ分别为方向角，方向余弦分别为cosα、cosβ、cosγ。而方向余弦即为cosα=x/|MN|，cosβ=y/|MN|，cosγ=z/|MN|。

举个例子：若设向量MN={1-2,3-2,0-√2}={-1,1,-√2},模|MN|=根号下[(-1)^2+1^2+(-√2)^2]=2，方向余弦cosα=-1/2，cosβ=1/2，cosγ=-√2/2。

方向余弦方向角的知识这是空间向量的一个基本概念问题。向量a={x,y,z}，量a°是向量a的单位向量，a°|=1。则a°=(cosα)i+(cosβ)j+(cosγ)k中,i,j,k是坐标单位向量；式中,α,β,γ就叫做向量的方向角；cosα,cosβ,cosγ就叫做方向余弦。空间向量的概念空间向量作为新加入的内容，在处理空间问题中具有相当的优越性，比原来处理空间问题的方法更有灵活性。

如把立体几何中的线面关系问题及求角求距离问题转化为用向量解决，如何取向量或建立空间坐标系，找到所论证的平行垂直等关系，所求的角和距离用向量怎样来表达是问题的关键。

三元函数的方向余弦怎么求

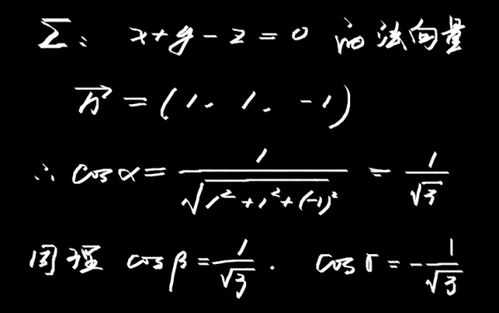
方向余弦计算公式为：cosa=ax/|a|。方向余弦是指在解析几何里，一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。

两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。

几何就是研究空间结构及性质的一门学科。

这个方向余弦怎么求

设：A（x1,y1,z1）,B（x2,y2,z2）.向量AB的方向余弦＝｛（x2-x1）/d,（y2-y1）/d.（z2-z1）/d｝其中，d＝|AB|＝√[（x2-x1）²+（y2-y1）²+（z2-z1）²]（x2-x1）/d＝cosα.,（y2-y1）/d＝cosβ..（z2-z1）/d＝cosγ其中：α,β,γ是向量AB分别与x轴。y轴，z轴所成的夹角[0≤α,β,γ≤π]故称方向余弦。

扩展资料：“方向余弦矩阵”是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。

方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。设有空间两点，若以P1为始点，另一点P2为终点的线段称为有向线段。通过原点作一与其平行且同向的有向线段，将与Ox,Oy,Oz三个坐标轴正向夹角分别记作α,β,γ。这三个角α,β,γ称为有向线段的方向角，其中0≤α≤π,0≤β≤π,0≤γ≤π。

若有向线段的方向确定了，则其方向角也是唯一确定的。方向余弦方法可以用来设定附体参考系B的取向，即刚体的取向。假设沿着参考系S的坐标轴的三个单位向量分别为，沿着参考系B的坐标轴的三个单位向量分别为。

定义与之间的方向余弦为；其中，是与之间的夹角。与之间的关系分别为、、。两个参考系的坐标轴所形成的矩阵称为“方向余弦矩阵” A ：。