如何比较斜率大小
如何比较斜率大小
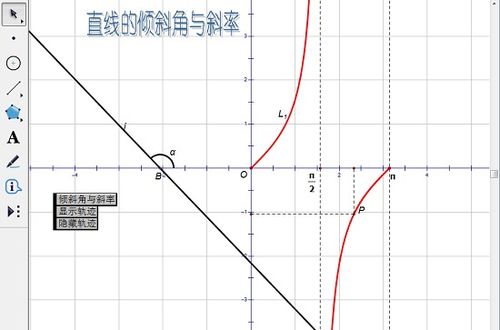
比较方法:1、当直线是由左下至右上延伸时坡度越陡的斜率越大,坡度越小时斜率越小。2、当直线是由左上向右下延伸时,坡度越大斜率越小,坡度越小的斜率越大。
其中第一种情况斜率始终为正,第二种情况中斜率始终为负,当直线平行于横坐标轴时斜率为0,当直线垂直于横坐标轴时斜率不存在。
斜率表示一条直线关于坐标轴倾斜程度的量,它通常用直线与坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。相关内容解释斜率用来量度斜坡的斜度。在数学上,直线的斜率处处相等,它是直线的倾斜程度的量度。透过代数和几何,可以计算出直线的斜率;曲线的上某点的斜率则反映了此曲线的变量在此点处的变化的快慢程度。
运用微积分可计算出曲线中的任一点的斜率。直线的斜率的概念等同土木工程和地理中的坡度。倾斜角不是90度的直线才有斜率。
斜率大小怎么比较
斜率表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
什么是斜率 斜率又称“角系数”,是一条直线对于横坐标轴正向夹角的正切,反映直线对水平面的倾斜度。
.一条直线与某平面直角坐标系横坐标轴正半轴方向所成的角的正切值即该直线相对于该坐标系的斜率.如果直线与x轴互相垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b,(斜截式)k即该函数图像的斜率。 规定平行于X轴的直线的斜率为零,平行于Y轴的直线的斜率不存在。对于过两个已知点(x1,y1)和(x2,y2)的直线,若x1≠x2,则该直线的斜率为k=(y1-y2)/(x1-x2)。
如何判断斜率的大小 1、当直线是由左下至右上延伸时坡度越陡的斜率越大、坡度越小时斜率越小 2、当直线是由左上向右下延伸时、坡度越大斜率越小,坡度越小的斜率越大. 其中第一中情况斜率始终为正,第二种情况中斜率始终为负.值得注意的是当直线平行于x轴时斜率为0,当直线垂直于x轴时斜率不存在。
曲线的斜率大小怎么看
看曲线的弯曲程度,其切线倾斜程度越大,斜率越大。先判断上面提到的角是锐角还是钝角,若是锐角,则越接近90°斜率越大,若是钝角,则越接近90°,斜率越小。
做曲线的切线,切线与x轴的正方向(注意是正方向)有个夹角,这个夹角的tan值就是这条切线的斜率。
曲线的斜率大小怎么看 导数即表示函数在某一点的切线的斜率。例如f'(x)=x^2,在x=4时,f'(x)=8,在x=0时,f'(x)=0,所以在x=0时,f(x)=x^2的切线可看作与x轴平行。 研究某一函数的导数很重要,因为它的几何意义是该函数曲线在这一点上的切线斜率,而斜率直接关系到在某一个区间函数的增减性。 当对于任意x∈(a,b)都有f'(x)>0时,函数f(x)在(a,b)是增函数。
而当对于任意x∈(a,b)都有f'(x)<0时,函数f(x)在(a,b)是减函数。
怎样判断斜率的大小?(急!)
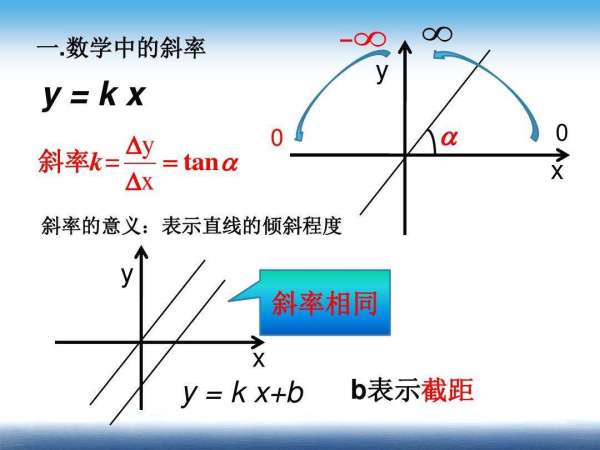 判断斜率就是判断K的大小.就是看直线和X轴的夹角问题.夹角越大,斜率越大.斜率也就是tan夹角的意思tan的图像在0到90°上是单调递增的.所以斜率大.角度大.至于如何判断.1.LZ如果方便就画出来2.主楼吧直线的公式变化成Y...
判断斜率就是判断K的大小.就是看直线和X轴的夹角问题.夹角越大,斜率越大.斜率也就是tan夹角的意思tan的图像在0到90°上是单调递增的.所以斜率大.角度大.至于如何判断.1.LZ如果方便就画出来2.主楼吧直线的公式变化成Y...判断斜率的大小的方法?
当斜率为负数时,如左图:则红色线斜率小,与纵轴的夹角小;当斜率为正数是,如右图:则红色线效率大,与纵轴的夹角小。比较两条线与纵轴的夹角,当交点不在纵轴时,如上右图,可以平移其中一条使二者在纵轴相交。
斜率为正时,夹角小则斜率大;斜率为负时,夹角小则斜率小。
如何判断直线的斜率的大小?

直线斜率公式:k=(y2-y1)/(x2-x1);如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
斜率反映直线对水平面的倾斜度。
一条直线与某平面直角坐标系横坐标轴正半轴方向所成的角的正切值即该直线相对于该坐标系的斜率。如果直线与x轴互相垂直,直角的正切值为tan90°,故此直线不存在斜率。扩展资料曲线的变化趋势仍可以用过曲线上一点的切线的斜率即导数来描述。导数的几何意义是该函数曲线在这一点上的切线斜率。
当f'(x)>0时,函数在该区间内单调递增,曲线呈向上的趋势;当f'(x)<0时,函数在该区间内单调减,曲线呈向下的趋势。在区间(a, b)中,当f''(x)<0时,函数在该区间内的图形是凸(从上向下看)的;当f''(x)>0时,函数在该区间内的图形是凹的。
免责声明:本站部分内容由用户自行上传,如权利人发现存在误传其作品,请及时与本站联系。
冀ICP备18013120号-1