方差怎么求?

方差怎么求?

方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。

总体方差计算公式：方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。

扩展资料：方差的性质1、设c是常数，则D（c）=02、设 X 与 Y 是两个随机变量，则D(X+Y)= D(X)+D(Y)+2Cov(X,Y)，D(X -Y)= D(X)+D(Y)-2Cov(X,Y)。特别的，当X，Y是两个不相关的随机变量则D(X+Y)=D(X)+D(Y)，D(X-Y)=D(X)+D(Y)，此性质可以推广到有限多个两两不相关的随机变量之和的情况。3、D(X)=0的充分必要条件是X以概率为1取常数值c，即X=c,a.s.其中E(X)=c。4、D(aX+bY)=a2DX+b2DY+2abCov(X,Y)。

方差怎么求

1，数学期望：公式离散型随机变量X的取值为，为X对应取值的概率，可理解为数据出现的频率，则：2，方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。[5]在实际计算中，我们用以下公式计算方差。

方差是各个数据与平均数之差的平方的和的平均数，即 ：，其中，x表示样本的平均数，n表示样本的数量，xi表示个体，而s^2就表示方差。

扩展资料：在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。

期望值并不一定包含于变量的输出值集合里。大数定律规定，随着重复次数接近无穷大，数值的算术平均值几乎肯定地收敛于期望值。

方差怎么算

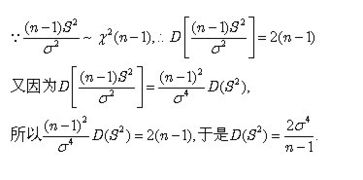
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。

在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。扩展资料方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。[5]在实际计算中，我们用以下公式计算方差。

方差是各个数据与平均数之差的平方的和的平均数，即，其中，x表示样本的平均数，n表示样本的数量，xi表示个体，而s^2就表示方差。而当用作为样本X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的倍，的数学期望才是X的方差，用它作为X的方差的估计具有“无偏性”，所以我们总是用来估计X的方差，并且把它叫做“样本方差”。方差是和中心偏离的程度，用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）并把它叫做这组数据的方差，记作S2。

在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。公式可以进一步推导为：。其中x为这组数据中的数据，n为大于0的整数。

方差的计算公式

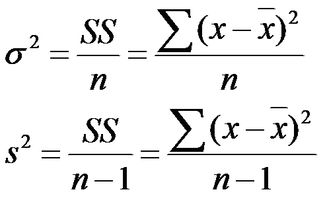
计算公式如下：1、方差公式：2、标准方差公式（1)：3、标准方差公式（2)：例如两人的5次测验成绩如下：X：50，100，100，60，50，平均值E(X)=72；Y：73，70，75，72，70平均值E(Y)=72。平均成绩相同，但X不稳定，对平均值的偏离大。

方差描述随机变量对于数学期望的偏离程度。

单个偏离是消除符号影响方差即偏离平方的均值，记为E(X)：直接计算公式分离散型和连续型。推导另一种计算公式得到：“方差等于各个数据与其算术平均数的离差平方和的平均数”。其中，分别为离散型和连续型计算公式。称为标准差或均方差，方差描述波动程度。

方差的概念：方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。

在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。

方差怎么计算 方差计算方法

1、方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。

在许多实际问题中，研究方差即偏离程度有着重要意义。

2、在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：如1、2、3、4、5 这五个数的平均数是3。方差就是1/5[（1-3）2+（2-3）2+（3-3）2+（4-3）2+（5-3）2]=2。